We have written much here in this magazine about the different properties of water. Some of them, such as surface tension, are of importance to the ability of aquatic fauna to function in their given environment. For example, surface tension permits water skaters to skate on the surface of the water where its habitat is neither the water below the surface nor the air above.
However, more than a purely physical phenomenon, osmosis is of importance for life itself, for no physical phenomenon has any greater importance in biology than does osmosis. Without osmosis neither animal cells nor plant cells could function. Not only this, osmosis also appears in many different guises in our everyday existence. So, what is this strange phenomenon?
We have written much here in this magazine about the different properties of water. Some of them, such as surface tension, are of importance to the ability of aquatic fauna to function in their given environment. For example, surface tension permits water skaters to skate on the surface of the water where its habitat is neither the water below the surface nor the air above.
However, more than a purely physical phenomenon, osmosis is of importance for life itself, for no physical phenomenon has any greater importance in biology than does osmosis. Without osmosis neither animal cells nor plant cells could function. Not only this, osmosis also appears in many different guises in our everyday existence. So, what is this strange phenomenon?
Osmosis
First, a definition: osmosis is the passage of a solvent from a region of high solvent concentration through a semi-permeable membrane to a region of low solvent concentration. In by far the majority of cases, especially biological, the solvent will be water.
Now, although this definition of osmosis is complete in itself, it is rather abstract for the general reader, and therefore, requires some amplification. What it means is this. If there is a concentrated solution of sugar, say, on one side of a suitable membrane (see below) and a less concentrated solution on the other side, then water will pass from the less concentrated side through to the other side where it will attempt to ‘thin’ the concentrated solution. The flow of water will cease when an equilibrium is established where the pressure on both sides of the membrane is the same.
The osmosis relationship
The basic relation for osmosis for a dilute solution is the van’t Hoff equation:
PV = npRT
where P is the osmotic pressure and np is the amount of solute in moles in a volume V of solvent. R, the gas constant, is 8.314 J K-1mol-1 and K is the absolute temperature.
For example, sucrose, C12H22O11, has molecular weight of 342.30. A 1% solution is water will therefore contain 1/342.30 0=0.00292 moles of sucrose.
This is very small compared with the 1000/18 = 55.5 moles of water in a litre of solution. From the molar point of view, it is a concentration of 1 in 19000 i.e. very dilute.
Assuming ideal conditions, the osmotic pressure produced by a 1% sucrose solution in water at room temperature (23ºC) is thus given by:-
P = 0.00292 x 8.314 x 296 / 0.001 Nm-2
= 7186 Nm-2
= ca. 0.72 atmospheres pressure
As one atmosphere can support a column of water 10m in height, this means that a 1% solution of sucrose could support a column of water 7.2 m in height. Thus, such a solution of sucrose could pump water to the top of a 7m high tree.
It is evident from the equation that if the osmotic pressure is known for a given concentration of solute, then it is possible to determine its molecular weight. It should be noted that this is not only true for water as the solute but also for other solvents.
For example, the molecular weight of polyvinylchloride (PVC) can be determined by osmotic pressure measurements in cyclohexanone solution.
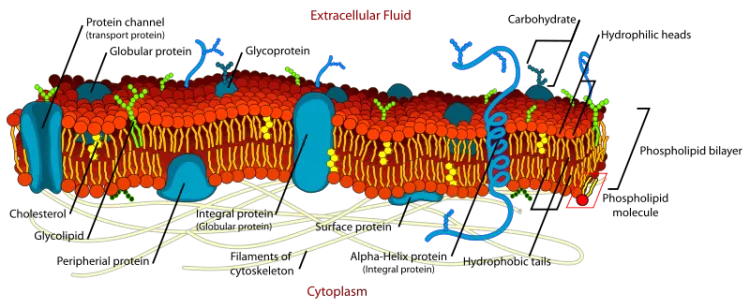
Semi-permeable membranes
Semi-permeable membranes are very thin films of a material, such as cellulose, that permit some molecules to pass through while hindering others. The molecules are separated from each other by their size, so that a small molecule such as water can easily pass through the membrane whilst large molecules such as sugars cannot. Semi-permeable membranes can occur in nature either as a plant cell walls or animal cell walls. From the point of view of osmosis, the main difference between these two is that a plant cell consists of a cell membrane supported by a strong cell wall while an animal cell has no cell wall, only a membrane.
For many technical purposes semi-permeable membranes can be tailored from synthetic polymers to permit specific molecules to pass through.

Picked vegetables
If you like your pickled gerkins or onions crisp, then use osmosis. When vegetables are put into brine, osmosis will occur through the semi-permeable cucumber or onion skin, so that the water inside the vegetables will pass out into the concentrated brine. This will give the pickles that desired crunchiness.
Preservation of food stuffs
If there are bacteria or yeast cells present in concentrated sugar solutions, then they will dehydrate due to osmosis and either die or become inactive. This is why sugar is used to preserve fruits in jams, etc.
Osmotic balance in animal cells
It is clear that if an organism is to function efficiently, if at all, then an osmotic balance must be maintained between the contents of its cells and their surroundings. This can be especially difficult for animal cells as, unlike plant cells, they do not have a strong supporting cell wall, only a cell membrane.
This means that if a blood cell, for example, is introduced into a hypertonic solution i.e. one with a higher concentration of solutes than that found within the cell cytoplasm, it will lose water by osmosis, and shrink. This can occur in the case of diabetes, where the sugar concentration in the blood becomes too high.
Burst
On the other hand, if the cell is in a hypotonic solution i.e. a solution with a lower concentration of solutes, then it will swell up and even burst under the osmotic pressure.
In either case there is a problem, so animal cells must always be bathed in an isotonic solution i.e. a solution having the same osmotic strength as their cytoplasm. The maintenance of such an isotonic solution is biologically very complex, being controlled by the kidneys under the influence of mechanisms in the brain which control the feeling of thirst, for example.
The challenge
The maintenance of osmotic balance is especially very difficult for marine animals. In most marine invertebrates, the salt content of the blood and body fluids is about the same as in seawater of average salinity. In the teleosts i.e. the bony fish, the salt concentration of the blood is only about 50% or less of the ambient salinity. This has physiological consequences, especially for aquatic animals migrating between seawater and freshwater.
The anadromous fish (from the Greek anadromos, running upwards) like the salmon, sturgeon, and sea lampreys migrate up rivers to breed in freshwater and their young then migrate to the sea. On the other hand, there are the catadromous fish (from the Greek katadromos, running down) which migrate down to the seas to breed but spend most of their adult life in freshwater, for example, the American and the European eels. It is also a problem for aquatic animals inhabiting estuaries where the salinity can change rapidly.

Because of the difference in salt concentration between blood and the ambient water, osmosis will cause teleost fish to lose water. Their internal salt concentration will therefore increase so that several mechanisms have evolved to counteract this problem. For example, most marine fish secrete salts across the gills as they only excrete very small amounts of urine.
Seabirds and sea turtles, for example, have also evolved various means of maintaining osmotic balance in their environments. Marine birds drink sea water to obtain water, but their kidneys are unable to produce concentrated urine. They therefore have special salt glands situated above the orbit of the eye, which can secrete salt. Marine mammals, on the other hand, do not have specialised glands for excreting salts. They avoid drinking seawater and get their water from the metabolism of food, depending on their kidneys for osmotic balance.
Reverse osmosis
Osmosis can be slowed, stopped and even reversed if sufficient pressure is applied to the concentrated side of the membrane. Reverse osmosis thus occurs when the water is forced through the membrane against the concentration gradient, from the lower concentration to the higher. Ions such as Na+, Ca++, and Cl-, and larger molecules such as sugars, urea and bacteria cannot pass through the semi-permeable membrane. The impurities will thus collect on one side of the membrane while clean water will collect on the other.
Reverse osmosis is therefore often used in water purification. It can be used, for example, to desalinate seawater, although it requires large amounts of energy. Pressures of up to 40 to 70 atmospheres are required because the natural osmotic pressure of 24 atmospheres arising from the salts concentration has to be overcome. As brackish water contains a much lower concentration of salts, the purification of fresh and brackish water requires much lower pressures of about 10 atmospheres.
It can also be used to remove water as an impurity from other liquids, for example from ethanol, or for removing medical and industrial contaminants from fresh water.
Dialysis
This is a very important application of osmosis, which is used for purifying blood with loss of kidney function. In a dialysis machine, the patent’s blood is passed through tubes made of a semi-permeable material. The tubes are flushed externally with a sterile solution of sugars and other components. The corpuscular cells of the blood, such as the red and white blood cells, are too big to pass through the membrane of the tubes. However, urea and salt can pass though into the sterile solution and are thereby removed from the blood.
Electricity from osmosis
An interesting project is being carried out in Norway to enable electricity to be produced from sea water by using osmotic pressure. When salt water and fresh water, from a stream or a river, are separated by a semi-permeable membrane, an osmotic pressure will occur. As stated above for reverse osmosis, this pressure can be up to 24 atmospheres. A column of water can thus be produced, which theoretically can be 240 m high.
The potential energy of this water column, like that from a dam, can be used to drive a turbine, which can then be used to drive a generator. The production of electricity by this method has no apparent ecological consequences, with the fresh water and salt water being mixed in the water column in the same way as would occur anyway at the mouth of the stream.
The potential for this form of ecologically-friendly energy is large, as such generators can be built anywhere that fresh water meets salt water, for example at the outflows from existing hydroelectric generators. ■